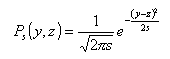 (s > 0,
y Î Â,
z Î Â)
(s > 0,
y Î Â,
z Î Â)
Een stochastisch proces is een drietal
{(W,A,P), (Xt : t³0), (E,E)}
waar (W,A,P) een kansruimte is, (E,E) een meetbare ruimte en (Xt : t³0) een familie stochastische variabelen op W met waarden in E. E heet de toestandsruimte voor het proces.
Zij I een niet-lege indexverzameling, dan noteren we met h(I) de verzameling der niet-lege eindige delen van I.
Beschouw de projecties pHJ : EH ® EJ voor J Ì H Î h(I). Veronderstel dat voor iedere i Î I een kansmaat Pi op E gegeven is. De familie der eindige productmaten PJ = ÄjÎJP j (geïndexeerd door J Î h(I)) is projectief in de zin dat voor J Ì H Î h(I):
PJ = PH ° (pHJ)-1.
De volgende stelling van Kolmogorov genereert nu ook 'productmaten' voor oneindige producten:
Zij E een volledige metrische ruimte met aftelbare basis en Borelstam E. Zij I een niet-lege indexverzameling. Voor iedere projectieve familie kansmaten {PJ; J Î h(I)} op {(EJ, EJ); J Î h(I)} bestaat er een unieke kansmaat PI op (EI, EI) zodat voor elke J Î h(I):
PJ = PI ° (pIJ)-1.
Zie bijvoorbeeld [Bauer1] p. 360.
We noteren voortaan
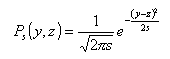 (s > 0,
y Î Â,
z Î Â)
(s > 0,
y Î Â,
z Î Â)
Definieer voor n Î N, 0 £ t1 < ... < tn de kansmaat P{t1,...,tn} op de Borelstam van Â{t1,...,tn} als volgt:
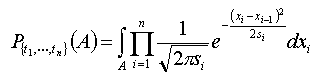
waar si = ti - ti-1, t0 = 0, x0 = x.
Dan is voor ieder Boreldeel B van Ân - 1:
P{t1,...,tn} (B ´ Â{ti}) = P{t1,...,tn} \ {ti}(B)
en dus is {P{t1,...,tn} ; n Î N, 0 £ t1 < ... < tn} een projectief systeem van kansmaten. Wegens stelling 2.1.2 bestaat er dan een kansmaat PÂ+ op (ÂÂ+, RÂ+) zodat
P{t1,...,tn} = PÂ+ ° p-1{t1,...,tn} (n Î N, 0 £ t1 < ... < tn)
De drager ÂÂ+ van deze kansmaat kan gevoelig verkleind worden via de stelling van Kolmogorov-Prokhorov:
Zij {(W,A,P), (Xt : t³0), (E,E)} een stochastisch proces zodanig dat er reële getallen a > 0, b > 1 en c > 0 bestaan met:
E[|Xs - Xt|a] £ c.|s - t|b (s, t ³ 0);
dan bestaat een stochastisch proces met dezelfde drager en toestandsruimte, en met variabelen (X't : t³0) zodanig dat voor iedere t £ 0: P(Xt ¹ X't) = 0 en dat bovendien voor iedere w Î W de functie t ® Xt(w) continu is op Â+.
Zie bijvoorbeeld [Bauer1] p. 371.
We noemen n-dimensionale Brownse beweging beginnend in x Î Ân elk stochastisch proces met toestandsruimte (Ân, Rn), met onafhankelijke componenten, met componentsgewijs eindigdimensionale verdelingen P{t1,...,tn} zoals in 2.1.3, waarvan de drager W bestaat uit de continue afbeeldingen Â+ ® Ân en waarvoor
Xt(w) = w(t) (wÎW, t ³ 0).
In [Bauer1], p. 396 wordt bewezen dat n-dimensionale Brownse beweging vertrekkend in x bestaat.
Voortaan noteren we de stochastische variabelen van Brownse beweging met b(t), de bijhorende kansmaat Px.
Op dezelfde drager W construeren we nu een nieuwe kansmaat P voor willekeurige maar vaste punten x en y in Ân en t ³ 0. Haar eindigdimensionale verdelingen zijn:
Ps1(x,x1) Ps2-s1(x1,x2) ... Psn-sn-1(xn-1,xn) Pt-sn(xn,y) / Pt(x,y) (0 £ s1 < ... < t)
Men ziet gemakkelijk dat dit voorschrift een projectief systeem van kansmaten definieert, zodat stelling 2.1.2 het bestaan van een kansmaat P garandeert met de gewenste verdelingen. De Brownse brug van x naar y voor tijdsduur t is nu een veelvoud van deze kansmaat, namelijk:
m0,x,y;t := Pt(x,y).P
De precieze reden voor de gewichtsfactor is propositie 2.1.7. Een integraal ten opzichte van de Brownse brug van x naar y in tijd t wordt genoteerd met het symbool Ex,y,0t[ ].
Tenslotte kunnen we W nog een derde maat meegeven. W is op te vatten als de productverzameling van een ruimte W0, de continue paden die uit de oorsprong vertrekken, met de ruimte Ân der beginpunten van paden. De eerste ruimte is de drager van P0 binnen W, de tweede heeft de Lebesguemaat. De productmaat van die twee noemen we de Wienermaat m0, en het overeenkomstige stochastische proces het Wienerproces. De paden van het Wienerproces en van de Brownse brug zijn in feite dezelfde als die van de Brownse beweging. Om het onderscheid te maken, zullen we ze echter noteren met de letter w.
Zij f: W ® Â+ meetbaar voor (b(s); 0 £ s £ t). Dan geldt:
![Ex[f(b)]=int_a Ex,0,a,t[f(om)]da](formule_2_1_7.gif)
Zij 0 < t1 < ... < tn < t; A1, ... , An Î R, f=1A1(b(t1)) ... 1An(b(tn)):
![Ex[f(b)] uitgewerkt, int f(om) d mu_0 uitgewerkt](formule_2_1_7b.gif)
Hiermee zijn de eerste twee beweringen aangetoond als f de indicator van een cilinder is. Voor willekeurige indicatoren gebruike men het lemma der monotone klassen van Dynkin, en een limietovergang geeft tenslotte de stelling voor willekeurige positieve meetbare functies.
De derde bewering volgt voor elementaire f uit de eindigdimensionale verdelingen van Brownse beweging en Brownse brug. Voor willekeurige f kan men opnieuw Dynkin en een limietovergang gebruiken.
////
Zij Ps(x,y) zoals in 2.1.3 en vat deze op als kern van een integraaloperator in de Hilbertruimte L2(Ân):
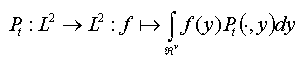
Dan is, voor elke t > 0, Pt een begrensde operator met norm hoogstens 1.
Zij f Î L2 positief en verder willekeurig. Dan is
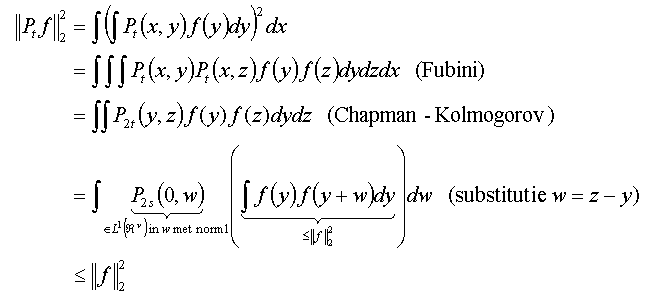
En dus is ||Pt|| £ 1.
////
De operatoren Pt werken ook in L¥ (en ook daar zijn ze begrensd, met norm 1). In het bijzonder laten ze dus het spoor van L¥ op L2 invariant.
Zij f een begrensde meetbare functie op Ân. Dan is Ptf continu op Ân.
Beschouw eerst het ééndimensionale geval. Voor willekeurige reële x en y (x £ y) is
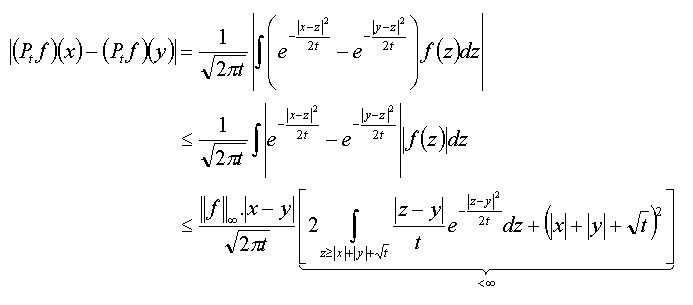
Het algemene, n-dimensionale geval kan hiertoe herleid worden:
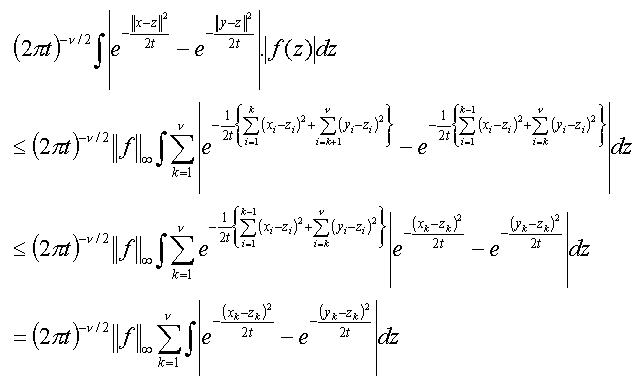
////
Deze continuïteit laat in bepaalde gevallen toe een L2-klasse te evalueren in één punt, door namelijk de unieke continue vertegenwoordiger van die klasse te beschouwen:
([Simon1] p. 36)
Zij f1,...,fn-1 Î L¥(Ân) en beschouw deze als (begrensde) vermenigvuldigingsoperatoren in L2. Zij fn Î L2(Ân) Ç L¥(Ân) en 0 < s1 < ... < sn. Dan geldt:
Ex[f1(b(s1))...fn(b(sn))] = (e-s1H0f1e-(s2-s1)H0...fn-1e-(sn-sn-1)H0fn)(x) (x Î Ân).
(Merk op dat de opeenvolgende transformaties van fn in het rechterlid steeds in L¥ Ç L2 blijven.)
De stochastische veranderlijken b(s1), b(s2) - b(s1), ... , b(sn) - b(sn-1) zijn onderling onafhankelijk. Hun verdeling wordt gegeven door:
Ps1(0,y1) Ps2-s1(0,y2) ... Psn-sn-1(0,yn) dny.
Hieruit volgt de verdeling van (b(s1), ... , b(sn)):
Ps1(0,x1) Ps2-s1(0,x2-x1) ... Psn-sn-1(0,xn-xn-1) dnx
of nog
Ps1(0,x1) Ps2-s1(x1,x2) ... Psn-sn-1(xn-1,xn) dnx.
Nu is
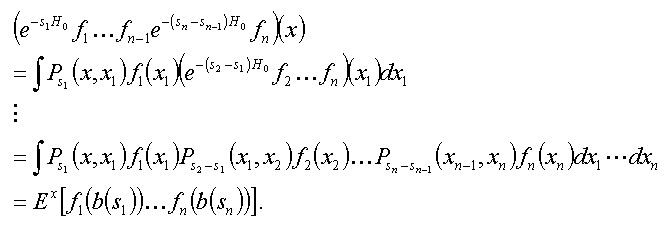
////
We zullen een verband leggen tussen de werking van operator-halfgroepen met een Hamiltoniaan als generator enerzijds en de integralen ten opzichte van de stochastische processen uit paragraaf 2.1 anderzijds. Dit zal ons vervolgens toelaten uitspraken te doen over de werking van die operator-halfgroepen.
Het volgende resultaat zal ons helpen uit te maken op welke Hamiltonianen de theorie van toepassing is.
Zij A een dicht gedefinieerde lineaire operator op een Hilbertruimte H. Dan genereert A een sterk continue positieve halfgroep als en slechts als A zelftoegevoegd en langs boven begrensd is.
Zie [Van Casteren1] p. 97.
Zij {Tn; n Î N} een familie begrensde operatoren van een Banachruimte X1, ||.||1 naar een Banachruimte X2, ||.||2. Veronderstel dat voor elke x Î X1 apart: limn®¥Tnx = 0. Dan is deze limiet uniform op compacte delen K van X1.
De banen {Tnx; n Î N} (x Î X1) zijn ieder afzonderlijk begrensd. Wegens de stelling van Banach-Steinhaus is dus de familie {Tn; n Î N} equicontinu (zie bijvoorbeeld [Rudin1] p. 43), zodat er een c > 0 bestaat met:
"x Î X1: supnÎN||Tnx||2 < c.||x||1.
Zij nu K een compact deel van X1. We bewijzen uit het ongerijmde dat
limn®¥supxÎK||Tnx||2 = 0.
Veronderstel namelijk het tegendeel. Dan bestond er een e > 0, een rij indices (kn)n en een rij vectoren (xn)n in K zodat
"n Î N: ||Tknxn||2 ³ e.
K is compact en dus heeft elke rij in K een verdichtingspunt in K. Zij x¥ Î K een verdichtingspunt van (xkn)n. Veronderstel, om de notatie te versoepelen, dat limn®¥xn = x¥ en dat "n Î N: ||Tnxn||2 > e.
Kies nu n0 Î N zo groot dat voor n ³ n0: ||xn - x¥||1 < e/2c.
Dan is supn³ n0||Tn(x¥ - xn)|| £ e/2 en dus is lim infn®¥Tnx¥ ³ e/2, in tegenspraak met de hypothese. De veronderstelling was dus vals.
////
Veronderstel dat A en B zelftoegevoegde langs onder begrensde operatoren op een separabele Hilbertruimte H zijn, zodanig dat A + B eveneens zelftoegevoegd is. Dan is
"t > 0, "f Î H: e-t(A+B)f = limn®¥(e-tA/ne-tB/n)nf.
| Noteer | St := e-t(A+B) | Ut := VtWt |
| Vt := e-tA | ft := Stf voor f Î D := D(A)ÇD(B) | |
| Wt := e-tB |
Zij D de Banachruimte D(A)ÇD(B) met norm |||f||| := ||(A+B)f|| + ||f||.
Beschouw de familie operatoren Tn:D®H gedefinieerd door:
Tnf := n(St/n - Ut/n)f (f Î D).
{Tn;n Î N} bestaat uit begrensde operatoren (|||.||| is sterker dan ||.||) en bovendien is voor elke f Î D:
| limn®¥||Tnf|| | = | limn®¥n||(St/n - Ut/n)f|| |
| = | lims®0||(1/s)(Ss-1)f - (1/s)(Us-1)f|| | |
| = | ||(A + B)f - lims®0(VsBf + Vs((1/s)(Ws-1) - B)f + (1/s)(Vs-1)f)|| | |
| = | ||(A + B)f - Bf - 0 - Af|| = 0. |
We kunnen dus lemma 2.3.2 toepassen, dat zegt dat voor compacte K Ì D:
limn®¥supxÎK n||(St/n - Ut/n)x|| = 0.
De afbeelding s®fs is continu (St is een continue halfgroep) en dus is K:={fs;0£s£t} compact in D.
Nu kunnen we verifiëren dat voor f Î D:
| limn®¥||(St - Ut/nn)f|| | = | limn®¥||Sj=0n-1Ut/nj(St/n - Ut/n)St/nn-j-1f|| |
| £ | supnÎN,0£j£n||Ut/n||jlim supn®¥sup0£s£t n||(St/n - Ut/n)fs|| |
Zijn nu a, b Î Â zodanig dat (A + a) en (B + b) positieve operatoren zijn; dan is sup ||Ut/n||j £ max(1,eta).max(1,etb) < ¥, en dus is de limiet 0. De stelling geldt dan ook voor algemene f Î H omdat D dicht is in H.
////
Zij V een continue reëelwaardige functie op Ân die klein wordt ver van de oorsprong, en beschouw de operator H = H0 + V op D(H0). Dan is voor iedere g Î L2(Ân) en voor bijna alle x Î Ân:
![(exp(-tH)g)(x)=E^x[g(b(t))exp(-int_0^tV(b(s))ds)]](formule_2_3_4.gif)
We bewijzen de stelling voor essentieel begrensde g. De veralgemening tot willekeurige g is dan nog slechts een triviale limietovergang.
Wegens de productformule van Lie-Trotter (2.3.3) is
(e-tHg)(x) = limn®¥((e-(t/n)H0e-(t/n)V)ng)(x)
waar de limiet in L2-zin voor functies van x moet geïnterpreteerd worden.
Wegens stelling 2.2.3 kan het rechterlid herschreven worden:
(...) = limn®¥Ex[g(b(t))e-(t/n)Sj=0n-1V(b(jt/n))]
Anderzijds convergeert dit laatste integrandum voor elk pad b(t) naar
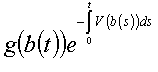
een convergentie die gedomineerd wordt door (e-tH0|g(b(t))|)e-t||V||¥ en die dus L1(W) is. Dit impliceert dat limiet en verwachtingswaarde mogen verwisseld worden. Maar nu hebben we een uitdrukking die in L2(Ân)-zin naar het linkerlid van het demonstrandum convergeert, en voor vaste x Î Ân naar het rechterlid. Dit voltooit het bewijs.
////
Zij V een continue, begrensde, reëelwaardige functie op Ân en H = H0 + V. Dan is voor iedere f en g in L2(Ân):
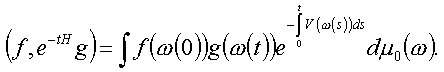
Dit is een onmiddellijk gevolg van stelling 2.3.4.
////
([Van Casteren1], p. 35)
Zij V een Borelmeetbare reëelwaardige functie op Ân en noem
![R_t(x,y)=E(x,0,y,t)[exp(-int_0^tV(omega(s))ds)]](formule_2_3_6.gif)
Veronderstel dat voor een zekere Borelmeetbare f:Ân ® C, x Î Ân en t > 0:
![E^x[exp(int_0^tV_(b(s))ds)|f(b(t)|]<oo](formule_2_3_6b.gif)
Dan is voor die x en t:
![int R_t(x,y)f(y)dyE^x[exp(-int_0^tV(b(s))ds)f(b(t)]](formule_2_3_6c.gif)
Noem Vk := min(V,k) (k > 0), en
![L := E^x[exp(-int_0^tV(b(s))ds)f(b(t)]](formule_2_3_6d.gif)
Wegens puntsgewijze convergentie, gedomineerd door
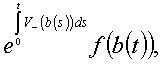
is
![L = lim_k exp(-kt)E^x[exp(int_0^t(k-V_k(b(s)))ds)f(b(t))]=lim_k lim r<t exp(-kt)E^x[exp(int_0^r(k-V_k(b(s)))ds)f(b(t))]](formule_2_3_6f.gif)
Verder is de Brownse beweging een Markovproces:
Ex[f(b(t))|b(s):0 £ s £ r] = Eb(r)[f(b(t-r))]] (0 < r < t)
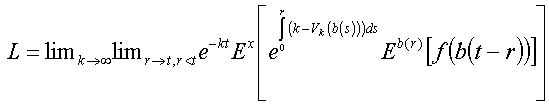
Per definitie is
![E^b(r)[f(b(t-r))]=int P_(t-r)(b(r),y)f(y)dy](formule_2_3_6h.gif)
voor F meetbaar t.o.v. de Brownse beweging tussen 0 en t.
Dit impliceert tenslotte dat
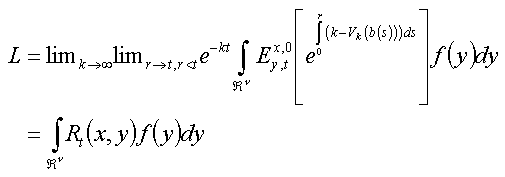
////
Zij V een continue, begrensde, reëelwaardige functie op Ân en zij H = H0 + V. Dan is e-tH een integraaloperator in L2(Ân) waarvoor een kern Rt(x,y) gegeven wordt door:
![R_t(x,y)=E(x,0,y,t)[exp(-int_0^tV(omega(s))ds)]](formule_2_3_6.gif)
Voor kwadratisch integreerbare f is de Wiener-integraal
eindig, dus wegens propositie 2.1.7, tweede uitspraak, is voor bijna alle x en y:
![E(x,0,y,t)[exp(int_0^tV_(omega(s))ds)f(omega(t))]](formule_2_3_7b.gif)
eindig. Combineer nu stelling 2.3.4 en stelling 2.3.6.
////
De strenge eisen op V in stelling 2.3.4 zijn slechts nodig om tot een gemakkelijke halfgroep te komen (voor willekeurige V, zelfs langs onder begrensd, ligt het niet voor de hand dat H0 + V een zelftoegevoegde operator is).
De natuurlijke klasse potentialen waarvoor stelling 2.3.4 geldt, wordt de Kato-klasse in n dimensies genoemd, en bestaat uit de functies V waarvoor:
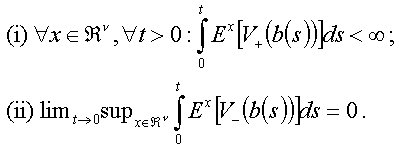
Deze klasse is zo scherp gekozen, dat nog net de volgende stelling kan bewezen worden (voor het bewijs: [Van Casteren1] p. 22):
Zij V een functie in de Kato-klasse, dan definieert het rechterlid van stelling 2.3.4 een sterk continue halfgroep van operatoren in L2, die de klasse der positieve reëelwaardige functies invariant laat en waarvan de generator een uitbreiding is van -H0 - V. Deze halfgroep en zijn generator zijn zelftoegevoegd.
////